Spherical perspective on learning with normalization layers

Simon Roburin    Yann de Mont-Marin    Andrei Bursuc    Renaud Marlet    Patrick Pérez    Mathieu Aubry

Neurocomputing 2022

Abstract

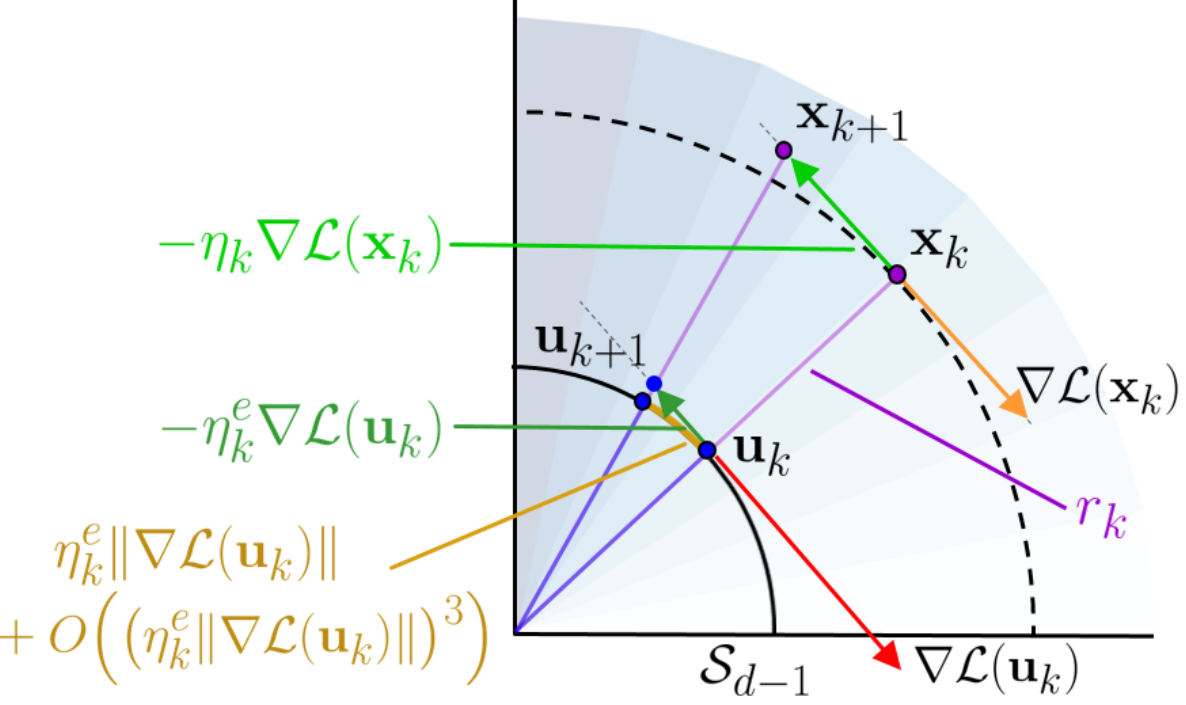
Normalization Layers (NLs) are widely used in modern deep-learning architectures. Despite their apparent simplicity, their effect on optimization is not yet fully understood. This paper introduces a spherical framework to study the optimization of neural networks with NLs from a geometric perspective. Concretely, the radial invariance of groups of parameters, such as filters for convolutional neural networks, allows to translate the optimization steps on the L2 unit hypersphere. This formulation and the associated geometric interpretation shed new light on the training dynamics. Firstly, the first effective learning rate expression of Adam is derived. Then the demonstration that, in the presence of NLs, performing Stochastic Gradient Descent (SGD) alone is actually equivalent to a variant of Adam constrained to the unit hypersphere, stems from the framework. Finally, this analysis outlines phenomena that previous variants of Adam act on and their importance in the optimization process are experimentally validated.

BibTeX

@article{spherical-adam-2022,
  author    = {Simon Roburin and
               Yann de Mont{-}Marin and
               Andrei Bursuc and
               Renaud Marlet and
               Patrick P{\'{e}}rez and
               Mathieu Aubry},
  title     = {Spherical perspective on learning with normalization layers},
  journal   = {Neurocomputing},
  volume    = {487},
  pages     = {66--74},
  year      = {2022}
}