Self-supervised learning with rotation-invariant kernels

Léon Zheng    Gilles Puy    Elisa Riccietti   Patrick Pérez    Rémi Gribonval

ICLR 2023

Abstract

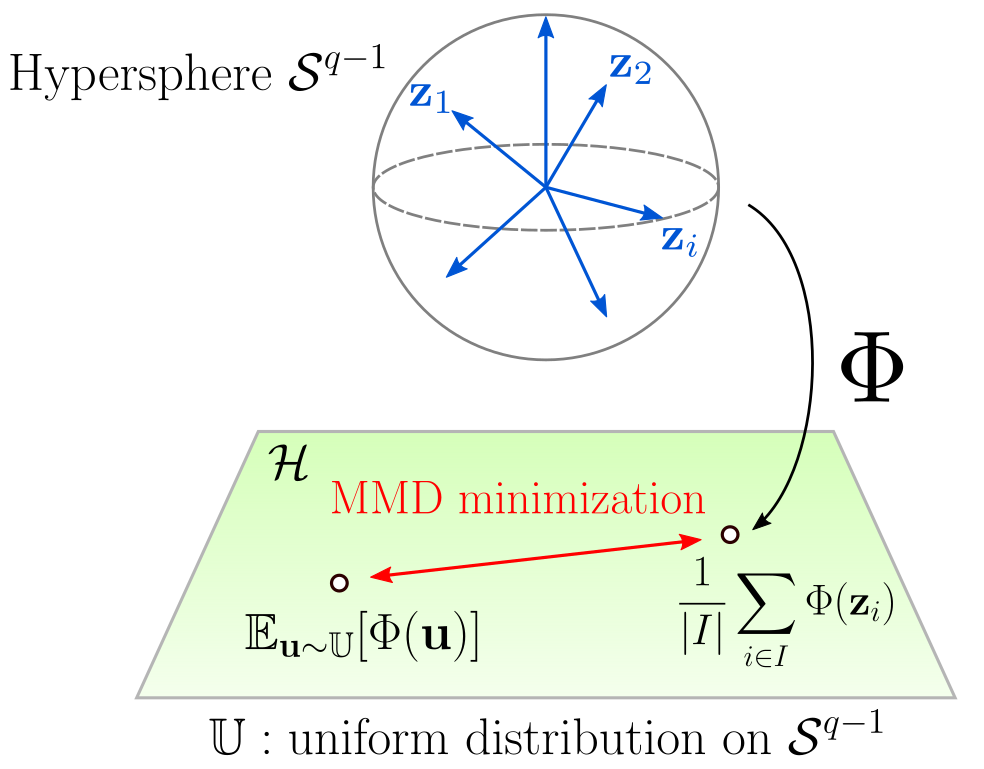
We introduce a regularization loss based on kernel mean embeddings with rotation-invariant kernels on the hypersphere (also known as dot-product kernels) for self-supervised learning of image representations. Besides being fully competitive with the state of the art, our method significantly reduces time and memory complexity for self-supervised training, making it implementable for very large embedding dimensions on existing devices and more easily adjustable than previous methods to settings with limited resources. Our work follows the major paradigm where the model learns to be invariant to some predefined image transformations (cropping, blurring, color jittering, etc.), while avoiding a degenerate solution by regularizing the embedding distribution. Our particular contribution is to propose a loss family promoting the embedding distribution to be close to the uniform distribution on the hypersphere, with respect to the maximum mean discrepancy pseudometric. We demonstrate that this family encompasses several regularizers of former methods, including uniformity-based and information-maximization methods, which are variants of our flexible regularization loss with different kernels. Beyond its practical consequences for state-of-the-art self-supervised learning with limited resources, the proposed generic regularization approach opens perspectives to leverage more widely the literature on kernel methods in order to improve self-supervised learning methods.

BibTeX

@inproceedings{
    zheng2023selfsupervised,
    title={Self-supervised learning with rotation-invariant kernels},
    author={L{\'e}on Zheng and Gilles Puy and Elisa Riccietti and Patrick Perez and R{\'e}mi Gribonval},
    booktitle={The Eleventh International Conference on Learning Representations },
    year={2023},
    url={https://openreview.net/forum?id=8uu6JStuYm}
}